Rozkład normalny
Gęstość prawdopodobieństwa Czerwona linia odpowiada standardowemu rozkładowi normalnemu. | |
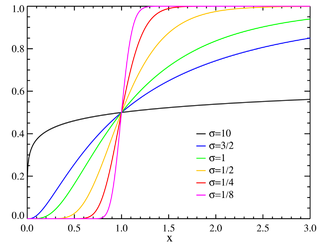
Dystrybuanta Kolory odpowiadają wykresowi powyżej | |
| Parametry | μ położenie (liczba rzeczywista) σ2 > 0 podniesiona do kwadratu skala (liczba rzeczywista) |
|---|---|
| Nośnik | 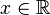 |
| Gęstość prawdopodobieństwa | 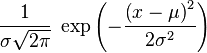 |
| Dystrybuanta |  |
| Wartość oczekiwana (średnia) |  |
| Mediana |  |
| Moda |  |
| Wariancja |  |
| Współczynnik skośności |  |
| Kurtoza |  |
| Entropia |  |
| Funkcja generująca momenty |  |
| Funkcja charakterystyczna |  |
| Odkrywca | Abraham de Moivre (1733)[1] |
Przyczyną jest jego częstość występowania w naturze. Jeśli jakaś wielkość jest sumą lub średnią bardzo wielu drobnych losowych czynników, to niezależnie od rozkładu każdego z tych czynników, jej rozkład będzie zbliżony do normalnego[2], stąd można go bardzo często zaobserwować w danych[3]. Ponadto rozkład normalny ma interesujące właściwości matematyczne, dzięki którym oparte na nim metody statystyczne są dość proste obliczeniowo[4].
Definicja rozkładu normalnego [edytuj]
Istnieje wiele równoważnych sposobów zdefiniowania rozkładu normalnego. Należą do nich: funkcja gęstości, dystrybuanta, momenty, kumulanty, funkcja charakterystyczna, funkcja tworząca momenty i funkcja tworząca kumulanty. Wszystkie kumulanty rozkładu normalnego wynoszą 0 oprócz pierwszych dwóch.Funkcja gęstości
Funkcja gęstości rozkładu normalnego ze średnią μ i odchyleniem standardowym σ (równoważnie: wariancją σ2) jest przykładem funkcji Gaussa. Dana jest ona wzorem: . Jeśli μ = 0 i σ = 1, to rozkład ten nazywa się standardowym rozkładem normalnym, jego funkcja gęstości opisana jest wzorem:
. Jeśli μ = 0 i σ = 1, to rozkład ten nazywa się standardowym rozkładem normalnym, jego funkcja gęstości opisana jest wzorem:We wszystkich rozkładach normalnych funkcja gęstości jest symetryczna względem wartości średniej rozkładu. Około 68,3% pola pod wykresem krzywej znajduje się w odległości jednego odchylenia standardowego od średniej, około 95,5% w odległości dwóch odchyleń standardowych i około 99,7% w odległości trzech (reguła trzech sigm). Punkt przegięcia krzywej znajduje się w odległości jednego odchylenia standardowego od średniej.
Dystrybuanta [edytuj]
Dystrybuanta jest definiowana jako prawdopodobieństwo tego, że zmienna X ma wartości mniejsze bądź równe x i w kategoriach funkcji gęstości wyrażana jest (dla rozkładu normalnego) wzorem:Funkcje tworzące [edytuj]
Funkcja charakterystyczna [edytuj]
Funkcją charakterystyczną rozkładu normalnego jestWłasności [edytuj]
- Jeśli
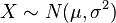 oraz
oraz  są liczbami rzeczywistymi, to
są liczbami rzeczywistymi, to 
- Jeśli
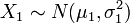 i
i 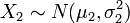 oraz zmienne
oraz zmienne  są niezależne, to
są niezależne, to 
- Jeśli
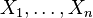 są niezależnymi zmiennymi losowymi o standardowym rozkładzie normalnym, to zmienna
są niezależnymi zmiennymi losowymi o standardowym rozkładzie normalnym, to zmienna 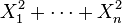 ma rozkład chi-kwadrat z
ma rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Parametry rozkładu [edytuj]
- wartość oczekiwana:

- mediana:

- wariancja:

- odchylenie standardowe:
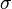
- skośność:

- kurtoza:
 (lub 3, przyjmując dawniej używaną definicję).
(lub 3, przyjmując dawniej używaną definicję).
Standaryzowanie zmiennych losowych o rozkładzie normalnym [edytuj]
Konsekwencją własności 1 jest możliwość przekształcenia wszystkich zmiennych losowych o rozkładzie normalnym do standardowego rozkładu normalnego.Jeśli X ma rozkład normalny ze średnią μ i wariancją σ2, wtedy:
Standardowy rozkład normalny został stablicowany i inne rozkłady normalne są prostymi transformacjami rozkładu standardowego. W ten sposób możemy używać tablic dystrybuanty rozkładu normalnego do wyznaczenia wartości dystrybuanty rozkładu normalnego o dowolnych parametrach.
Generowanie wartości losowych o rozkładzie normalnym [edytuj]
W symulacjach komputerowych zdarza się, że potrzebujemy wygenerować wartości zmiennej losowej o rozkładzie normalnym. Istnieje kilka metod, najprostszą z nich jest odwrócenie dystrybuanty standardowego rozkładu normalnego. Są jednak metody bardziej wydajne, jedną z nich jest transformacja Boxa-Mullera, w której dwie zmienne losowe o rozkładzie jednostajnym (prostym do wygenerowania — patrz generator liczb losowych) są transformowane na zmienne o rozkładzie normalnym.Transformacja Boxa-Mullera jest konsekwencją własności 3 i faktu, że rozkład chi-kwadrat z dwoma stopniami swobody jest rozkładem wykładniczym (łatwym do wygenerowania).
Centralne twierdzenie graniczne [edytuj]
Jedną z najważniejszych własności rozkładu normalnego jest fakt, że, przy pewnych założeniach, rozkład sumy dużej liczby zmiennych losowych jest w przybliżeniu normalny. Jest to tak zwane centralne twierdzenie graniczne.W praktyce twierdzenie to ma zastosowanie jeśli chcemy użyć rozkładu normalnego jako przybliżenia dla innych rozkładów.
- Rozkład dwumianowy z parametrami
 jest w przybliżeniu normalny dla dużych
jest w przybliżeniu normalny dla dużych  i
i  nie leżących zbyt blisko 1 lub 0. Przybliżony rozkład ma średnią równą
nie leżących zbyt blisko 1 lub 0. Przybliżony rozkład ma średnią równą  i odchylenie standardowe
i odchylenie standardowe 
- Rozkład Poissona z parametrem
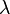 jest w przybliżeniu normalny dla dużych wartości
jest w przybliżeniu normalny dla dużych wartości 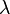 . Przybliżony rozkład normalny ma średnią
. Przybliżony rozkład normalny ma średnią  i odchylenie standardowe
i odchylenie standardowe 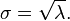
Nieskończona podzielność [edytuj]
Rozkład normalny należy do rozkładów mających własność nieskończonej podzielności.Występowanie [edytuj]
Rozkład normalny (lub wielowymiarowy rozkład normalny) jest często stosowanym założeniem, w praktyce jednak nigdy nie jest ściśle realizowany. Rozkład normalny ma bowiem niezerową gęstość prawdopodobieństwa dla dowolnej wartości zmiennej losowej, podczas gdy w rzeczywistości zmienne są zawsze ograniczone, a często nieujemne.Mimo to rzeczywisty rozkład jest często bardzo zbliżony do normalnego, stąd zwykle zakłada się, że zmienna ma rozkład normalny. Nie należy jednak robić tego bez sprawdzenia jak wielkie są rozbieżności. Rozkłady dalekie od normalnego (np. z elementami odstającymi) mogą sprawić, że wyniki metod statystycznych będą mylnie interpretowane.
Przykładem są tu metody regresji liniowej oraz korelacji Pearsona, które, choć zdefiniowane dla dowolnych rozkładów, mają sensowną interpretację tylko dla wielowymiarowego rozkładu normalnego wektora próbki. Jeśli w próbce występują elementy odstające, co jest szczególnym przypadkiem rozkładu dalekiego od normalnego, korelacja może przyjąć dowolną wartość między −1 a +1, bez względu na rzeczywistą zależność między zmiennymi losowymi. Także regresja będzie dawała błędne rezultaty.
Inteligencja [edytuj]
Inteligencja mierzona testami inteligencji uważana jest za zmienną o rozkładzie normalnym. Oczywiście w praktyce testy dają wyniki skwantowane, a nie ciągłe. W dodatku ich wyniki są ograniczone do pewnego przedziału. Przybliżenie jest jednak wystarczające.Wzrost [edytuj]
Podobnie wzrost człowieka może być uznany w przybliżeniu za zmienną o rozkładzie normalnym. Musimy wtedy oczywiście założyć, że wartość oczekiwana rozkładu wynosi np. 170 cm, aby przypadek "ludzi o ujemnym wzroście" miał znikomo małe prawdopodobieństwo.Natężenie źródła światła [edytuj]
Natężenie światła z pojedynczego źródła zmienia się w czasie i zazwyczaj zakłada się, że ma rozkład normalny. Jednak zgodnie z mechaniką kwantową światło jest strumieniem fotonów. Zwykłe źródło światła, świecące dzięki termicznej emisji, powinno świecić w krótkich przedziałach czasu zgodnie z rozkładem Poissona. W dłuższym przedziale czasowym (dłuższym niż czas koherencji) dodawanie się do siebie niezależnych zmiennych prowadzi w przybliżeniu do rozkładu normalnego.Błędy pomiaru [edytuj]
Wielokrotne powtarzanie tego samego pomiaru daje wyniki rozrzucone wokół określonej wartości. Jeśli wyeliminujemy wszystkie większe przyczyny błędów, zakłada się, że pozostałe mniejsze błędy muszą być rezultatem dodawania się do siebie dużej liczby niezależnych czynników, co daje w efekcie rozkład normalny. Odchylenia od rozkładu normalnego rozumiane są jako wskazówka, że zostały pominięte błędy systematyczne. To stwierdzenie jest centralnym założeniem teorii błędów.Rozkład wykładniczy
Z Wikipedii, wolnej encyklopedii
Gęstość prawdopodobieństwa | |
Dystrybuanta | |
| Parametry |  odwrotność parametru skali (liczba rzeczywista) odwrotność parametru skali (liczba rzeczywista) |
|---|---|
| Nośnik |  |
| Gęstość prawdopodobieństwa |  |
| Dystrybuanta |  |
| Wartość oczekiwana (średnia) |  |
| Mediana |  |
| Moda |  |
| Wariancja |  |
| Współczynnik skośności | 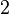 |
| Kurtoza | 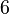 |
| Entropia | 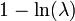 |
| Funkcja generująca momenty | 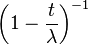 |
| Funkcja charakterystyczna | 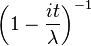 |
| Odkrywca | |
Dystrybuanta tego rozkładu to prawdopodobieństwo, że obiekt jest w stanie Y.
Innymi słowy, jeżeli w jednostce czasu ma zajść 1/λ niezależnych zdarzeń, to rozkład wykładniczy opisuje odstępy czasu pomiędzy kolejnymi zdarzeniami.








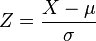

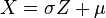




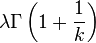

 dla
dla 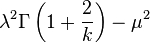
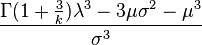
![\tfrac{-6\Gamma_1^4+12\Gamma_1^2\Gamma_2-3\Gamma_2^2
-4\Gamma_1\Gamma_3+\Gamma_4}{[\Gamma_2-\Gamma_1^2]^2}](http://upload.wikimedia.org/math/0/b/0/0b0e0d9f2fa9b72c9fe3cc32a3962d6d.png)
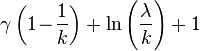
 osobników (porównaj
osobników (porównaj 
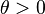


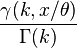





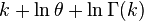







![\frac{1}{x\sigma\sqrt{2\pi}}\exp\left[-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}\right]](http://upload.wikimedia.org/math/b/3/f/b3f2a95779f28c24a5a265ba6498ceec.png)
![\frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]](http://upload.wikimedia.org/math/2/5/3/253b03515b12e5affd383a2c2f022145.png)