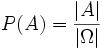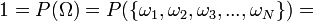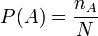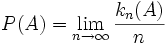Prawdopodobieństwo
Z Wikipedii, wolnej encyklopedii
Prawdopodobieństwo – ogólne określenie wielu pojęć matematycznych, służących do - mówiąc w uproszczeniu - mierzenia szansy zajścia zdarzenia.Wg najpopularniejszej w rachunku prawdopodobieństwa definicji Kołmogorowa prawdopodobieństwo to miara probabilistyczna, tj. funkcja P przypisująca każdemu zdarzeniu losowemu
 pewną nieujemną liczbę rzeczywistą i mająca następujące własności:
pewną nieujemną liczbę rzeczywistą i mająca następujące własności: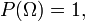 gdzie
gdzie 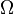 jest przestrzenią zdarzeń elementarnych
jest przestrzenią zdarzeń elementarnych- prawdopodobieństwo sumy przeliczalnego zbioru zdarzeń parami rozłącznych jest równe sumie prawdopodobieństw tych zdarzeń:
 nazywa się prawdopodobieństwem zdarzenia
nazywa się prawdopodobieństwem zdarzenia 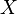 .
. Spis treści[pokaż] |
Prawdopodobieństwo w ujęciu potocznym [edytuj]
Potocznie prawdopodobieństwo to pojęcie określające oczekiwania co do rezultatu danego zdarzenia, którego wyniku nie znamy (niezależnie od tego czy jest ono w jakimś sensie zdeterminowane czy też nie, ani też od tego czy miało miejsce w przeszłości czy dopiero się wydarzy). Jeśli jakieś mające nastąpić zdarzenie (np. rzut kostką), może przyjąć kilka rezultatów (liczba oczek), to jeden z rezultatów (liczba oczek większa od 1) możemy opisać jako uznawany przez nas za bardziej prawdopodobny od drugiego (liczba oczek równa 1), jeżeli na podstawie jakiejś przesłanki (np. poprzednich doświadczeń), nasze oczekiwania co do wystąpienia rezultatu A są większe niż co do wystąpienia rezultatu B.Definicja prawdopodobieństwa w oparciu o subiektywne odczucia jest oczywiście zupełnie nieprzydatna dla celów praktycznych. Brak sformalizowanej definicji musieli szczególnie dotkliwie odczuwać pierwsi "praktycy" teorii prawdopodobieństwa, czyli nałogowi hazardziści. Jeśli rzucimy monetą 50 razy i za każdym razem wyrzucimy reszkę, nie oznacza to, iż jest bardziej prawdopodobne, że przy 51 rzucie wypadnie orzeł.
Definicja klasyczna (Laplace'a) [edytuj]
Definicje [edytuj]
Sposób liczenia prawdopodobieństwa z poprzedniego przykładu podał po raz pierwszy Pierre Simon de Laplace w roku 1812. Definicję tę nazywamy klasyczną, choć tak naprawdę jest to twierdzenie, którego dowód możemy znaleźć poniżej. Twierdzenie to brzmi:- Prawdopodobieństwem zajścia zdarzenia A nazywamy iloraz liczby zdarzeń sprzyjających zdarzeniu A do liczby wszystkich możliwych przypadków, zakładając, że wszystkie przypadki wzajemnie się wykluczają i są jednakowo możliwe.
- Oznaczmy zbiór wszystkich możliwych przypadków przez
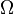 . Elementami zbioru
. Elementami zbioru 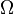 są zdarzenia elementarne
są zdarzenia elementarne 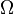 , zaś zbiór
, zaś zbiór 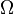 to zbiór zdarzeń elementarnych. Zbiór zdarzeń sprzyjających A będzie w takim wypadku podzbiorem zbioru
to zbiór zdarzeń elementarnych. Zbiór zdarzeń sprzyjających A będzie w takim wypadku podzbiorem zbioru  .
.
- Prawdopodobieństwo zajścia zdarzenia A możemy zapisać w postaci:
- gdzie
 oznacza liczbę elementów (moc) zbioru
oznacza liczbę elementów (moc) zbioru  , zaś
, zaś  liczbę elementów (moc) zbioru
liczbę elementów (moc) zbioru 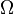 .
.
Problemy definicji klasycznej [edytuj]
Definicja klasyczna pozwala obliczać prawdopodobieństwo w prostych przypadkach, jednak zawiera szereg wad: nie można jej stosować dla zbiorów nieskończonych, a przede wszystkim zawiera błąd logiczny. Zdarzenia elementarne muszą być jednakowo możliwe, co znaczy przecież to samo co jednakowo prawdopodobne. Okazuje się więc, że w definicji użyto pojęcia, które jest definiowane.Podobne problemy dotyczą prawdopodobieństwa geometrycznego - zauważył to Joseph Louis Francois Bertrand opisując paradoks nazywany jego nazwiskiem – paradoks Bertranda.
Przykład [edytuj]
Przykład: Rzucamy sześcienną kostką. Jakie jest prawdopodobieństwo, że liczba oczek będzie większa od 5?Odpowiedź: Zbiór zdarzeń elementarnych
 zatem liczba możliwych zdarzeń elementarnych
zatem liczba możliwych zdarzeń elementarnych  . Zbiór zdarzeń sprzyjających
. Zbiór zdarzeń sprzyjających  , liczba zdarzeń sprzyjających
, liczba zdarzeń sprzyjających  . Prawdopodobieństwo zajścia zdarzenia
. Prawdopodobieństwo zajścia zdarzenia  wynosi:
wynosi:Dowód [edytuj]
Niech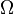 będzie zbiorem zdarzeń elementarnych, a
będzie zbiorem zdarzeń elementarnych, a 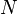 jego mocą. Znaczy to, że
jego mocą. Znaczy to, że  , gdzie
, gdzie  to zdarzenie elementarne.
to zdarzenie elementarne.Załóżmy, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne (czyli P({ωi}) = P({ωj}) dla każdego
 . Oznaczmy
. Oznaczmy  będące prawdopodobieństwem dowolnego zdarzenia elementarnego), wychodząc z II i III aksjomatu Kołmogorowa otrzymujemy:
będące prawdopodobieństwem dowolnego zdarzenia elementarnego), wychodząc z II i III aksjomatu Kołmogorowa otrzymujemy: , którego prawdopodobieństwa poszukujemy będzie zbiorem zdarzeń elementarnych o mocy
, którego prawdopodobieństwa poszukujemy będzie zbiorem zdarzeń elementarnych o mocy  . Dla uproszczenia przyjmijmy że są to zdarzenia o numerach od 1 do
. Dla uproszczenia przyjmijmy że są to zdarzenia o numerach od 1 do  , czyli:
, czyli: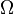 dostajemy:
dostajemy:- Prawdopodobieństwo zdarzenia A wyraża się ilorazem mocy tego zbioru oraz mocy zbioru zdarzeń elementarnych
Prawdopodobieństwo geometryczne [edytuj]
Definicja klasyczna nie pozwala obliczać prawdopodobieństwa w przypadku, gdy zbiory i
i 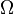 są nieskończone, jeśli jednak zbiory te mają interpretację geometryczną, zamiast liczebności zbiorów można użyć miary geometrycznej (długość, pole powierzchni, objętość).
są nieskończone, jeśli jednak zbiory te mają interpretację geometryczną, zamiast liczebności zbiorów można użyć miary geometrycznej (długość, pole powierzchni, objętość).Przykład: z przedziału
![[0,4]\;](http://upload.wikimedia.org/math/1/b/5/1b56e16e6df6ef3aeca826141dbe59bc.png) wybieramy losowo punkt. Jakie jest prawdopodobieństwo, że wybrany punkt będzie należał do przedziału
wybieramy losowo punkt. Jakie jest prawdopodobieństwo, że wybrany punkt będzie należał do przedziału ![[1,2]\;](http://upload.wikimedia.org/math/1/8/5/185e7dcc34b67daab24a59dcd26739dd.png) ?
?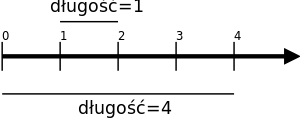
Długości przedziałów wynoszą odpowiednio: | [0,4] | = 4 i | [1,2] | = 1. Zatem prawdopodobieństwo opisanego zdarzenia wynosi:
Definicja częstościowa (von Misesa) [edytuj]
Inną próbę sformułowania definicji prawdopodobieństwa podjął w 1931 roku Richard von Mises. Zaproponował, żeby zdefiniować prawdopodobieństwo jako granicę ciągu częstości: to liczba rezultatów sprzyjających zdarzeniu
to liczba rezultatów sprzyjających zdarzeniu  po
po  próbach.
próbach.Definicja ta nie mówi jednak nic o warunkach istnienia granicy i dlatego nie spełnia wymogów formalnych.
Przykład [edytuj]
Przypuśćmy, że ktoś zaproponował nam grę losową: "orzeł wygrywamy, reszka przegrywamy". Na pewno zanim zagramy, będziemy chcieli zbadać jakie są szanse wygranej, przeprowadzamy więc doświadczenie, polegające na wielokrotnym rzucie monetą. Rzucamy 100 razy, orzeł wypadł 48 razy, a więc w 48/100 = 0,48 wszystkich przypadków. Kontynuujemy doświadczenie, po 1000 rzutów orzeł wypadł 508 razy, czyli w 508/1000 = 0,508 wszystkich przypadków. Znaleziona przez nas wielkość to częstość wypadania orła. Gdyby powtarzać dalej to doświadczenie, stosunek ten dążyłby do wartości 0,5, będącej prawdopodobieństwem wylosowania orła według definicji von Misesa.Aksjomatyczna definicja prawdopodobieństwa (Kołmogorowa) [edytuj]
Nową definicję prawdopodobieństwa podał w 1933 Andriej Kołmogorow, który korzystając z teorii miary zaksjomatyzował teorię prawdopodobieństwa.- Załóżmy, że
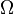 jest zbiorem zdarzeń elementarnych
jest zbiorem zdarzeń elementarnych 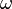 , zaś
, zaś  jest σ-ciałem na zbiorze
jest σ-ciałem na zbiorze 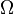 . Prawdopodobieństwem nazywamy funkcję
. Prawdopodobieństwem nazywamy funkcję  spełniającą następujące warunki:
spełniającą następujące warunki:  dla każdego
dla każdego 
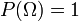
- jeśli
 jest dowolnym ciągiem podzbiorów
jest dowolnym ciągiem podzbiorów  parami rozłącznych, to:
parami rozłącznych, to:
Alternatywną aksjomatyzację pojęcia prawdopodobieństwa podał Richard Threlkeld Cox.
Bezpośrednie konsekwencje definicji:
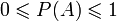

- (odwrotna implikacja nie jest prawdziwa -
 nie implikuje
nie implikuje  )
)
- (odwrotna implikacja nie jest prawdziwa -
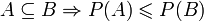 (monotoniczność)
(monotoniczność)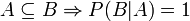
 gdzie
gdzie  oznacza zdarzenie losowe przeciwne do
oznacza zdarzenie losowe przeciwne do